Каталог статей

Відкриття несумірних відрізків у Стародавній Греції

Ще стародавні греки, вчені так званої Піфагорійської школи відкрили в геометрії несумірні відрізки. Це відкриття було поворотним пунктом в історії античної математики. Важко переоцінити значення цього відкриття. Його можна порівняти тільки із значенням неевклідової геометрії для розвитку науки XIX—XX ст.

Ми не знаємо точно, як саме прийшли до відкриття несумірності. Це могло статися:

в геометрії при знаходженні спільної міри сторони і діагоналі квадрата;
в теорії музики при спробах поділити октаву пополам, тобто фактично знайти середнє геометричне число 1 і 2;
нарешті, в арифметиці могла виникнути потреба точно знайти дріб, квадрат якого дорівнює 2.

Як би там не було, мова йшла про відшукання і дослідження величини корінь з 2. Відкриття факту, що між двома відрізками — стороною і діагоналлю квадрата — не існує спільної, навіть як завгодно малої, міри, привело до справжньої кризи основ грецької математики. Піфагорійці, відкривши в VI ст. до н. е. існування несумірних відрізків, тримали це відкриття в таємниці, оскільки воно суперечило їх ідеалістичному вченню про гармонію чисел у навколишньому світі.

Незабаром було встановлено, що несумірність діагоналі й сторони квадрата не є винятком, що існують й інші величини, відношення яких не можна подати відношенням двох (цілих) чисел. Феодор з Кірени (V ст. до н. е.) показав, що сторони квадратів, площі яких дорівнюють 3, 5, 6, 7, 8, 10, 11, 12, 1З, 14, 15, 17, несумірні з стороною одиничного квадрата. Його учень і друг Теетет показав що корінь з n виражає довжину, несумірну з одиницею, якщо n — не точний квадрат. Він також вперше дістав ірраціональність виду

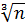
Замість того щоб розширити поняття числа, греки дійшли висновку, що треба відокремити вивчення цілих чисел від геометрії (оскільки цілих чисел і дробів виявилось недостатньо для вимірювання геометричних фігур), встановити точну межу між арифметикою і геометрією.

Відкриття давньогрецького математика Піфагора Самоського (бл. 577 — бл. 500 до н. е.) і його учнів потягло за собою ряд глибоких досліджень грецьких геометрів про несумірні відрізки. Вінцем цих досліджень є V книга «Начал» Евкліда, в якій викладено загальну теорію відношень. X книга присвячена квадратичним ірраціональностям: Евклід побудував за допомогою циркуля і лінійки усі ірраціональності, що виникають у процесі розв’язування квадратних рівнянь.

Відома задача «про подвоєння куба», тобто знаходження ребра куба, який за об’ємом був би в два рази більший від заданого куба, привела греків до ірраціональностей вищого порядку; цю задачу вони розв’язали також геометрично і за допомогою побудови довели існування несумірних відрізків вищого порядку.

Відкриттю несумірних величин надавали важливого значення ще в давнину. Так, видатний давньогрецький філософ Арістотель (384—322 до н. е.) зазначав, що воно викликало здивування, як і всяке справжнє наукове відкриття.

Але деякі математики-ідеалісти у факті несумірності вбачали «прірву, через яку ні обчислення, ні логіка не спроможні були перекинути міст». Факт існування несумірних відрізків не гальмував розвитку геометрії. Греки розробили теорію відношень відрізків, яка враховувала можливість їх несумірності; вони вміли порівнювати такі відношення за величиною і виконувати над ними арифметичні дії (в суто геометричній формі).

Щоб позбутися ірраціональних чисел, греки використовували їх наближення, досить точні для практичних обчислень. Проте, хоч Герон Александрійський (І ст. н. е.) при обчисленні площ добуває квадратний корінь з добутку чисел, а Діофант Александрійський (III ст. н. е.) говорить уже про числа нераціональні, однак ідея того, що відношення довжин несумірних відрізків можна розглядати як число, в грецькій математиці не була усвідомлена до кінця.