Тисячи шляхів ведуть до помилки, до істини – тільки один.

                             Жан-Жак Руссо. 

                З античних часів математику вважають наукою точною, що не терпить помилок, вимагає ясності понять та тверджень, нічого не сприймає без доведень, проголошує красу та велич логічних міркувань. За словами Ж.Фабра "математика - дивовижна вчителька в мистецтві спрямовувати думки, наводити порядок там, де вони не впорядковані, викорчовувати безглуздя, фільтрувати брудне і наводити ясність". Помилки в міркуваннях, найчастіше  виникають через порушення законів формальної логіки, основи якої заклав визначний давньогрецький філософ Арістотель (праці "Категорії", "Про тулмачення", "Перша аналітика", "Друга аналітика", "Топіка"). Помилки, пов'язані з порушенням законів логіки  та законів математики бувають двох типів: паралогізми і софізми.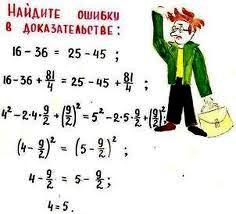 

Паралогізми (з грецької - неправильне) - це хибне міркування, логічна помилка, допущена не навмисне, а через втрату послідовності в міркуваннях чи порушення одного з законів логіки. Паралогізми в математиці неприпустимі, бо де є місце помилці, там вже немає місця математиці. Зовсім інша ситуація з софізмами.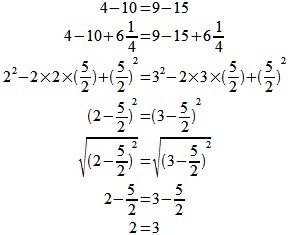 

Софізми (з грецької -хитрий викрутас, вигадка, хитрий умовивід) - це міркування навмисне побудовані так, що вони містять логічну помилку і, звичайно, приводять до хибних висновків. Засновником школи софістів був давньогрецький філософ Протогор із  Адбери (бл. 480   - бл.410 до р. х.). Введення софізмів сприяло вдосконавленню ораторського мистецтва, підвищенню логічної культури мислення. Щоправда, пізніше в деяких філософів-софістів мистецтво софістики перетворилося на суперечку заради суперечки. Різні приклади софізмів наводить у своїх діалогах Платон (427 -347 до р. х.). Евклід ( 1V ст. До р. х.)створив дивовижний збірник "Псевдарій",який на жаль не дійшов до нас. Це був перший збірник саме математичних софізмів та парадоксів. Вперше аналіз та класифікацію софізмів  дав Арістотель у трактаті "Про софістичні спростування". На сьогодні софізми, і зокрема математичні, навчають мислити , доводити й спростовувати, чітко висловлювати свої думки; вони здивовують та захоплюють, дають поштовх для творчості, пошуку нового, відкриттів. Найчастіше софізми та паралогізми виникають, коли міркування порушують закони логіки: закон тотожності, закон суперечності, закон виключного третього, закон достатьньої підстави.

Закон тотожності  вимагає, щоб одна і та сама думка, яка наводиться в даному умовиводі, при повторенні мала однаковий зміст. При порушенні цього закону виникають помилки трьох видів: еквівокація, логомахія і амфіболія. Суть помилки еквівокації (з латинської - такі, що звучать однаково) в тому, що в міркуваннях використовують багатозначне ім'я предмета, то в одному, то в іншому значенні, вважаючи це ім'я однозначним. Наприклад: "Кожен метал є елементом. Латунь - метал. Отже, латунь є елементом." Неправильний висновок зумовлений помилкою еквівокації. У першому реченні слово "метал" використано у значенні хімічного елемента, в другому йдеться про сплав металів - речовину, яка має фізичні властивості металу: ковкість, електропроводність, металевий блиск тощо. У математиці помилка еквівокації маайже неможлива і завжди очевидна, оскільки вимога відсутності омонімії не допускає двозначності понять,використаних у математичних міркуваннях. Іноді під час дискусії один з її учасників використовує деяке багатозначне ім'я в іншому значенні ніж його опонент. Суперечка може бути нескінченою. Такий диспут називається логомахією (з грецької - словесна суперечка ). Логомахією називається також диспут,який не дає нічого суттєво важливого.

Амфіболія (з грецької - двозначність) виникає, коли використовують речення, яке можна тулмачити по-різному. Наприклад, відома фраза "Страчувати не можна помилувати" допускає два протележні тулмачення.

Закон суперечності (латинська назва - Lex contradictionis) полягає в тому, що не можуть бути одночасно істиними два протележні висловлювання про один і той самий об'єкт, взятий в один і той самий час і в одному й тому самому розумінні. Закон суперечності пов'язаний з так званими контрарними (з латинської - протележний) протележностями. Це вид протележностей, коли зіставляється загальностведжувальне і загально-заперечувальне висловлювання: "Всі ромби - опуклі чотирикутники", "Жоден ромб не є опуклим чотирикутником". Цікаво, що обидві  контрарні протилежності можуть бути хибними: "Всі прості числа непарні", "Всі прості числа парні", тобто існує третя можливість - "Існує єдине парне просте число". Оперуючи з контрарними протележностями, потрібно дотримуватися правил: 1) з істиності одного з контрарних висловлювань випливає хибність іншого; 2) з хибності одного з контрарних висловлювань не можна встановити істинність контрарного щодо нього висловлювання (воно може бути як істинним, так і хибним). У цому фундаментальне значення закону суперечності для людського мислення - з хибності випливає і істина , і хибність.

 Закон виключеного третього ( латинська назва - Lex exclusi tertii sive medii inter duo contradictoria) стверджує, що з двох суперечливих висловлювань, де розглядається один і той самий об'єкт в один і той самий час, одне обов'язково істинне. Цей закон поширюється на так звані контрадикторні (з латинської - суперечливий) проте-лежності. Це вид протележностей, коли зіставляються: загальностверджувальне і частиннозаперечувальне висловлювання ( "Всі парні числа складені", "Деякі парні числа не є складеними" ) або загальнозаперечувальне і частинностверджувальне ( "Навколо будь-якого неправиль-ного багатокутника не можна описати коло", "Навколо де-яких неправильних багатокутників можна описати коло" ). Одне з контрадикторних висловлювань обов'язково істинне, інше - неодмінно хибне, третього бути не може. Цей закон відіграє в математиці дуже важливу роль. Він лежить в основі опосередкованих доведень.

 Закон достатньої підстави  вимагає, щоб кожна істинна думка була обгрунтована іншими думками, істинність яких доведено. За законом достатньої підстави наші висловлювання повинні бути внутрішньо пов'язаними, випливати одне з одного (наступне з попереднього), обгрунтовувати одне одне.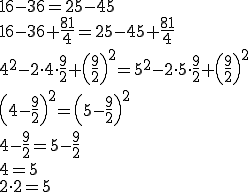

                Отож бо помилки йдуть від порушень законів логіки, або інших математичних законів. Паралогізми чекають на неуважних або недостатньо натренованих у складному мистецтві міркувань. Софізми - навмисне розставлені логічні пастки. Але бувають й інші, тривожніші, справді катастрофічні ситуації в пізнавальній діяльності людини. Іноді правильні формально-логічні міркування приводять до результатів, які не узгоджуються з загальноприйнятою думкою, здаються безглуздими. Це парадокси (з грецької - несподіваний, дивовижний). Давньогрецький філософ Діодор Кронос, не розв'язавши однієї з найдавніших логічних загадок - парадоксу Евбуліда, помер від розпачу, а інший філософ Філет Косський, зазнавши такої самої невдачі, кінчив життя самогубством. Ще складнішими були парадокси (апорії) Зенона Елейського. Парадокси виникали і виникають в усіх галузях людської діяльності. Вивчення парадоксів, спроби їх розгадати й знешкодити мають не тільки теоритичний інтерес. Якщо в логіці Й математиці можливі парадокси, то де гарантія, що в складну програму ЕОМ, яка керує, наприклад деякими життєвоважливими процесами, не прослизне один з них? Тоді такий парадокс може обернутися трагічними подіями в реальності. Що ж до софізмів, то вони безпечні, захоплюючі,  виконують навчальну та розважальну функції.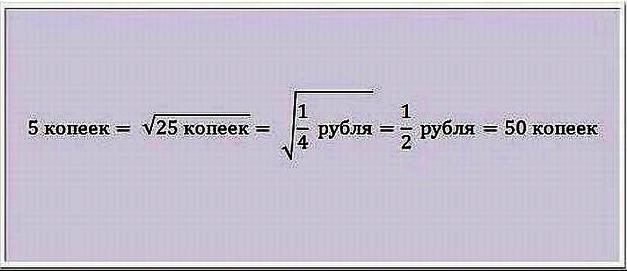